Thuật toán Quick Sort là một trong các thuật toán sắp xếp cực hiệu quả, có khả năng ứng dụng cao nhất hiện nay. Hãy cùng Vietnix tìm hiểu chi tiết về Quick Sort là gì và cách triển khai Quick Sort trong các môi trường ngôn ngữ lập trình khác nhau từ C++14, Java, Python cho đến C#, Javascript.
Thuật toán QuickSort là gì?
Thuật toán QuickSort là một dạng thuật toán sắp xếp, được xây dựng dựa trên nguyên tắc thuật toán chia để trị. QuickSort hoạt động dựa trên việc phân chia các mảng dữ liệu thành các nhóm phần tử nhỏ hơn. Tuy nhiên, các lập trình viên sẽ cần một thời gian đáng kể để làm quen, nghiên cứu và học cách “làm chủ” Thuật toán QuickSort. Các phiên bản QuickSort khác nhau sẽ chọn pivot theo những cách khác nhau.
- Luôn chọn phần tử đầu tiên làm trục.
- Luôn chọn phần tử cuối cùng làm trục.
- Chọn một phần tử ngẫu nhiên làm trục quay.
- Chọn trung vị làm trục.
Quá trình đóng vai trò quan trọng trong QuickSort là phân vùng (). Phân vùng là việc đặt một mảng và một phần tử x của mảng làm trụ, đặt x vào đúng vị trí của nó trong mảng đã sắp xếp và đặt tất cả các phần tử nhỏ hơn x và trước x, đặt tất cả các phần tử lớn hơn x và sau x.
Minh họa cách triển khai thuật toán QuickSort
Dưới đây sẽ là minh họa chung cho khả năng sắp sếp của thuật toán QuickSort.
Thuật toán phân vùng
Có nhiều cách để thực hiện thuật toán phân vùng. Chúng ta bắt đầu từ phần tử ngoài cùng bên trái và theo dõi chỉ số của các phần tử nhỏ hơn (hoặc bằng) là i. Trong quá trình duyệt, nếu tìm thấy một phần tử nhỏ hơn, bạn cần hoán đổi phần tử hiện tại với arr [i]. Nếu không, bạn nên bỏ qua phần tử hiện tại.
Pseudo code cho hàm QuickSort function:
/* low –> Starting index, high –> Ending index */
quickSort(arr[], low, high) {
if (low < high) {
/* pi là partitioning index, arr [pi] hiện ở đúng vị trí */
pi = partition(arr, low, high);
quickSort(arr, low, pi – 1); // Trước pi
quickSort(arr, pi + 1, high); // Sau pi
}
}Pseudo code cho phân vùng ()
/* Hàm này nhận phần tử cuối cùng làm pivot, đặt phần tử pivot vào đúng vị trí và đặt tất cả các phần tử nhỏ hơn (nhỏ hơn pivot) ở bên trái của pivot, còn các phần tử lớn hơn ở bên phải của pivot*/.
partition (arr[], low, high)
{
// pivot (Phần tử được đặt đúng vị trí)
pivot = arr[high];
i = (low – 1) // Index của smaller element và indicates the
// vị trí bên phải của pivot được tìm thấy cho đến nay
for (j = low; j <= high- 1; j++){
// Nếu element hiện tại nhỏ hơn pivot
if (arr[j] < pivot){
i++; // chỉ số increment index của smaller element
hoán đổi arr[i] và arr[j]
}
}
swap arr[i + 1] and arr[high])
return (i + 1)
}Minh họa phân vùng – partition()
Consider: arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[h] = 70
Khởi tạo index của smaller element, i = -1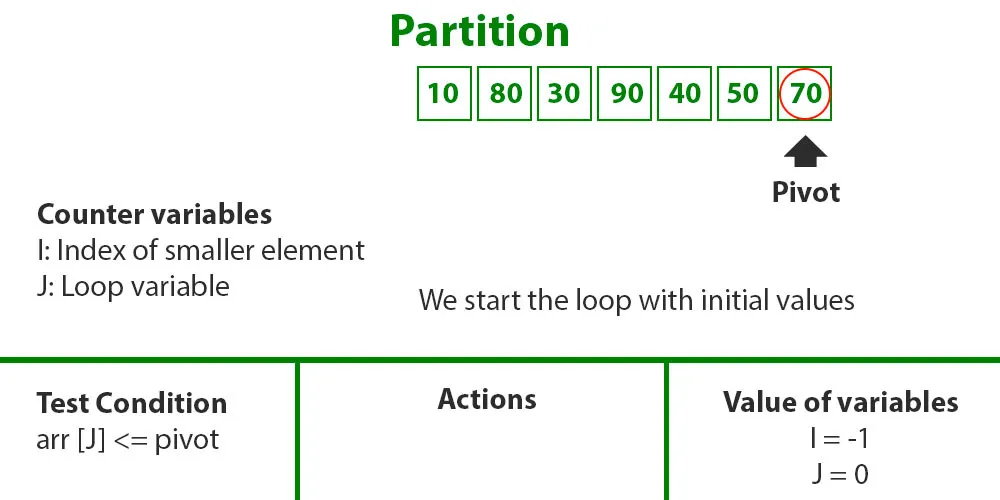
Traverse elements from j = low to high-1
j = 0: Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // Không hay đổi gì vì i và j giống nhau
j = 1: Since arr[j] > pivot, do nothing
j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // Hoán đổi 80 và 30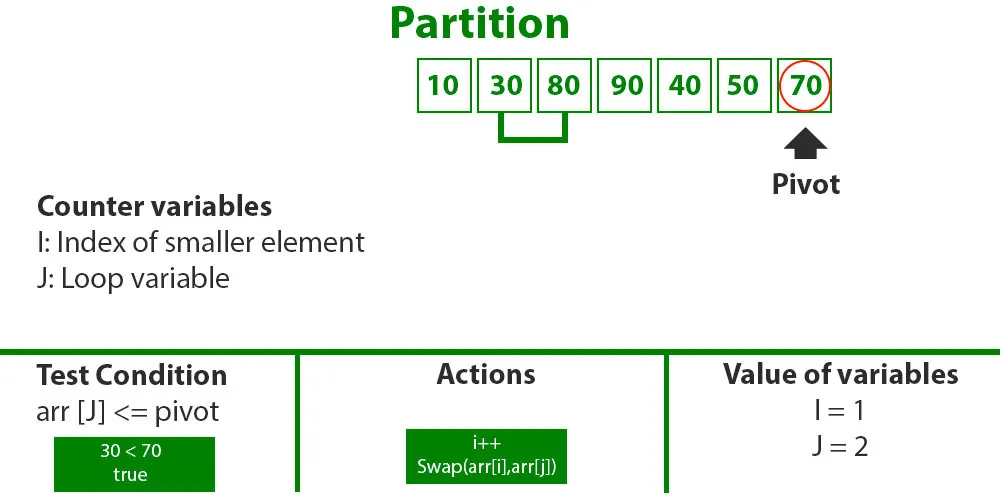 
- j = 3 : Since arr[j] > pivot, do nothing // Không thay đổi i và arr[]
- j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
- i = 2
- arr[] = {10, 30, 40, 90, 80, 50, 70} // Hoán đổi 80 và 40
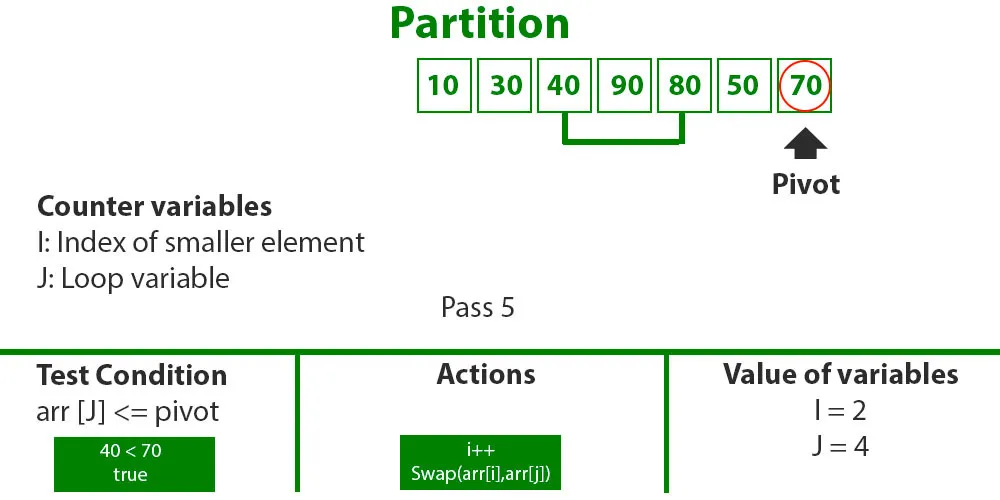
- j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j]
- i = 3
- arr[] = {10, 30, 40, 50, 80, 90, 70} // Hoán đổi 90 và 50
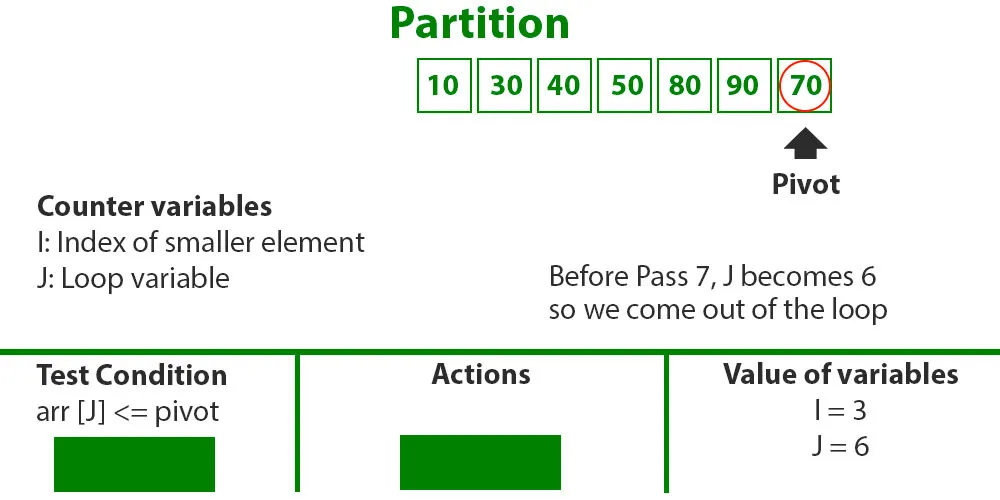
- Thoát khỏi vòng lặp vì j cao hơn -1.
- Cuối cùng, bạn đặt trục ở vị trí chính xác bằng cách hoán đổi arr[i+1] and arr[high] (or pivot) arr[] = {10, 30, 40, 50, 70, 90, 80} // Hoán đổi 80 và 70
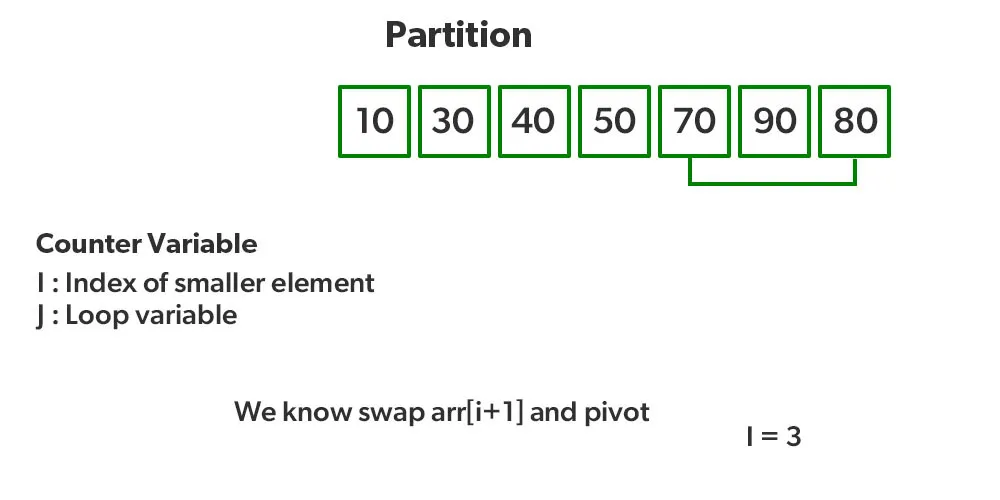
- Giờ phần tử 70 đã ở đúng vị trí, tất cả các phần tử < 70 nằm trước nó còn các phần tử > 70 nằm đằng sau.
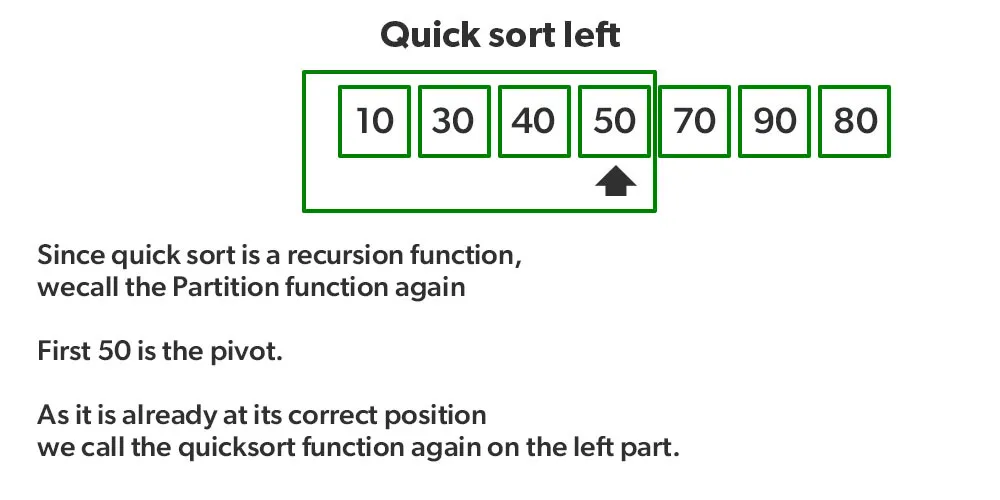
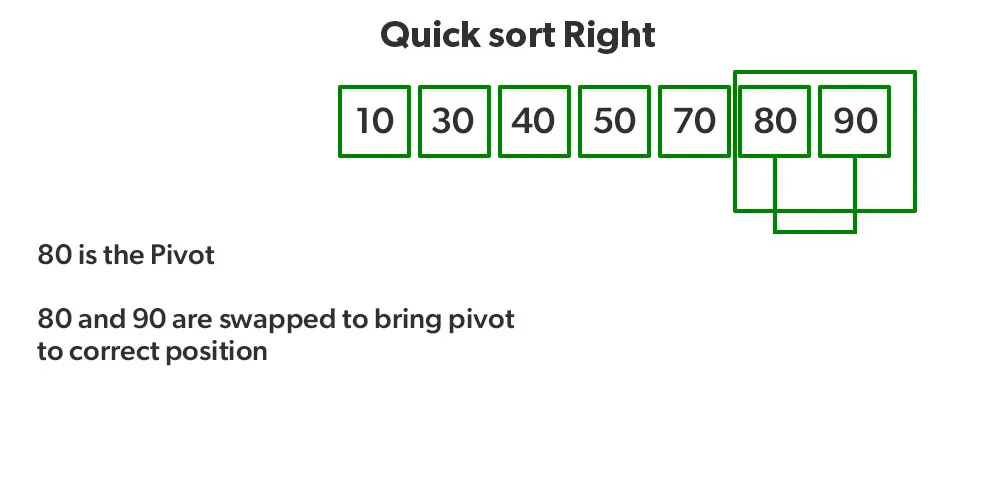
- Vì QuickSort là một hàm đệ quy, ta gọi lại hàm phân vùng ở các phân vùng bên trái và bên phải.
- Gọi chức năng ở phần bên phải và hoán đổi 80, 90.
Cách triển khai QuickSort cho 5 ngôn ngữ lập trình phổ biến nhất hiện nay
Dưới đây là cách triển khai QuickSort cho một số ngôn ngữ lập trình phổ biến.
Triển khai QuickSort trong C++14
/* C++ implementation of QuickSort */
#include <bits/stdc++.h>
using namespace std;
//Một utility function để hoán đổi 2 elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
/* Hàm này nhận element cuối cùng làm pivot, địa điểm pivot element xoay
ở vị trí chính xác của nó trong được sắp xếp mảng và đặt tất cả nhỏ hơn (nhỏ hơn pivot)
ở bên trái của pivot và tất cả các phần tử lớn hơn ở bên phải pivot*/
int partition (int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index của smaller element và indicates
//vị trí bên phải pivot được tìm thấy
for (int j = low; j <= high - 1; j++)
{
// Nếu current element là nhỏ hơn pivot
if (arr[j] < pivot)
{
i++; // increment index của element nhỏ hơn
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* Main function của implements QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver Code
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
cout << "Sorted array: \n";
printArray(arr, n);
return 0;
}QuickSort trong Java
// Java implementation of QuickSort
import java.io.*;
class GFG{
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/* Hàm này nhận phần tử cuối cùng làm pivot, địa điểm phần tử xoay ở vị trí chính xác của nó trong được sắp xếp mảng và đặt tất cả nhỏ hơn (nhỏ hơn pivot) ở bên trái của pivot và tất cả các phần tử lớn hơn ở bên phải pivot */
static int partition(int[] arr, int low, int high)
{
// pivot
int pivot = arr[high];
// Index of smaller element and
// indicates the right position
// of pivot found so far
int i = (low - 1);
for(int j = low; j <= high - 1; j++)
{
// If current element is smaller
// than the pivot
if (arr[j] < pivot)
{
// Increment index of
// smaller element
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
/* Chức năng chính thực hiện QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index
*/
static void quickSort(int[] arr, int low, int high)
{
if (low < high)
{
// pi is partitioning index, arr[p]
// is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to print an array
static void printArray(int[] arr, int size)
{
for(int i = 0; i < size; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver Code
public static void main(String[] args)
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.println("Sorted array: ");
printArray(arr, n);
}
}Bạn có thể tìm hiểu thêm về ngôn ngữ này trong bài tìm hiểu ngôn ngữ lập trình Java cho người mới của Vietnix.
Triển khai QuickSort trong Python 3
# Python3 implementation of QuickSort
# Chức năng tìm vị trí phân vùng phân vùng def (mảng, thấp, cao):
# Chọn phần tử ngoài cùng bên phải làm pivot
pivot = array[high]
# Con trỏ cho phần tử lớn hơn
i = low - 1
# Đi qua tất cả các yếu tố
# So sánh từng phần tử với pivot
for j in range(low, high):
if array[j] <= pivot:
# If element smaller than pivot is found
# swap it with the greater element pointed by i
i = i + 1
# Swapping element at i with element at j
(array[i], array[j]) = (array[j], array[i])
# Hoán đổi phần tử pivot với phần tử lớn hơn chỉ định
(array[i + 1], array[high]) = (array[high], array[i + 1])
# Trả lại vị trí từ nơi phân vùng được thực hiện
return i + 1
# Chức năng thực hiện QuickSort
def quick_sort(array, low, high):
if low < high:
#Tìm phần tử trục sao cho
# element smaller than pivot are on the left
# element greater than pivot are on the right
pi = partition(array, low, high)
# Recursive call on the left of pivot
quick_sort(array, low, pi - 1)
# Recursive call on the right of pivot
quick_sort(array, pi + 1, high)
# Driver code
array = [ 10, 7, 8, 9, 1, 5]
quick_sort(array, 0, len(array) - 1)
print(f'Sorted array: {array}')Nếu bạn đang tìm hiểu về Python có thể tham khảo bài viết về Python là gì và ứng dụng của ngôn ngữ lập trình Python.
Triển khai QuickSort trong C#
// C# implementation of QuickSort
using System;
class GFG
{
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/* Hàm này nhận phần tử cuối cùng làm pivot, địa điểm phần tử xoay ở vị trí chính xác của nó trong được sắp xếp mảng và đặt tất cả nhỏ hơn (nhỏ hơn pivot) ở bên trái của pivot và tất cả các phần tử lớn hơn ở bên phải pivot*/
static int partition(int[] arr, int low, int high)
{
// pivot
int pivot = arr[high];
// Index of smaller element and
// indicates the right position
// of pivot found so far
int i = (low - 1);
for (int j = low; j <= high - 1; j++)
{
// If current element is smaller
// than the pivot
if (arr[j] < pivot)
{
// Increment index of
// smaller element
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
/* Chức năng chính thực hiện QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index
*/
static void quickSort(int[] arr, int low, int high)
{
if (low < high)
{
// pi is partitioning index, arr[p]
// is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to print an array
static void printArray(int[] arr, int size)
{
for (int i = 0; i < size; i++)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
// Driver Code
public static void Main()
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int n = arr.Length;
quickSort(arr, 0, n - 1);
Console.Write("Sorted array: ");
printArray(arr, n);
}
}Triển khai QuickSort trong Javascript
<script>
// Javascript implementation of QuickSort
// A utility function to swap two elements
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/* Hàm này nhận phần tử cuối cùng làm pivot, địa điểm phần tử xoay ở vị trí chính xác của nó trong được sắp xếp mảng và đặt tất cả nhỏ hơn (nhỏ hơn pivot) ở bên trái của pivot và tất cả các phần tử lớn hơn ở bên phải pivot*/
function partition(arr, low, high) {
// pivot
let pivot = arr[high];
// Index of smaller element and
// indicates the right position
// of pivot found so far
let i = (low - 1);
for (let j = low; j <= high - 1; j++) {
// If current element is smaller
// than the pivot
if (arr[j] < pivot) {
// Increment index of
// smaller element
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
/* Chức năng chính thực hiện Quick Sort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index
*/
function quickSort(arr, low, high) {
if (low < high) {
// pi is partitioning index, arr[p]
// is now at right place
let pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to print an array
function printArray(arr, size) {
for (let i = 0; i < size; i++)
document.write(arr[i] + " ");
document.write("<br>");
}
// Driver Code
let arr = [10, 7, 8, 9, 1, 5];
let n = arr.length;
quickSort(arr, 0, n - 1);
document.write("Sorted array: <br>");
printArray(arr, n);Triển khai QuickSort bằng cách sử dụng phần tử đầu tiên làm trụ:
C++
#include <iostream>
#include <algorithm>
using namespace std;
int partition(int arr[], int low, int high)
{
int i = low;
int j = high;
int pivot = arr[low];
while (i < j)
{
while (pivot >= arr[i])
i++;
while (pivot < arr[j])
j--;
if (i < j)
swap(arr[i], arr[j]);
}
swap(arr[low], arr[j]);
return j;
}
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot - 1);
quickSort(arr, pivot + 1, high);
}
}
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
int main()
{
int arr[] = {4, 2, 8, 3, 1, 5, 7,11,6};
int size = sizeof(arr) / sizeof(int);
cout<<"Before Sorting"<<endl;
printArray(arr, size);
quickSort(arr, 0, size - 1);
cout<<"After Sorting"<<endl;
printArray(arr, size);
return 0;
}Python3
# Chức năng tìm vị trí phân vùng
def partition(arr, l, h):
low, high = l, h
if l != h and l < h:
# Chọn phần tử ngoài cùng bên trái làm trục
pivot = arr[l]
low = low+1
# Qua tất cả các yếu tố
# So sánh từng phần tử với pivot
while low <= high:
if arr[high] < pivot and arr[low] > pivot:
arr[high], arr[low] = arr[low], arr[high]
if not arr[low] > pivot:
low += 1
if not arr[high] < pivot:
high -= 1
arr[l], arr[high] = arr[high], arr[l]
# Trả lại vị trí từ nơi phân vùng được thực hiện
return high
# Chức năng thực hiện quicksort
def quick_sort(array, low, high):
if low < high:
# Find pivot element such that
# element smaller than pivot are on the left
# element greater than pivot are on the right
pi = partition(array, low, high)
# Recursive call on the left of pivot
quick_sort(array, low, pi - 1)
# Recursive call on the right of pivot
quick_sort(array, pi + 1, high)
# Driver code
array = [ 1, 7, 8, 9, 1, 2]
quick_sort(array, 0, len(array) - 1)
print(f'Sorted array: {array}')Output
Before Sorting
4 2 8 3 1 5 7 11 6
After Sorting
1 2 3 4 5 6 7 8 11Phân tích QuickSort
Thời gian thực hiện bởi QuickSort có thể được viết như sau:
T(n) = T(k) + T(n-k-1) + (n)Hai thuật ngữ đầu tiên dành cho hai cuộc gọi đệ quy, thuật ngữ cuối dành cho tiến trình phân vùng. (Trong đó: k là số phần tử nhỏ hơn pivot).
Thời gian thực hiện bởi QuickSort phụ thuộc vào mảng đầu vào và chiến lược phân vùng. Sau đây là ba trường hợp:
Trường hợp xấu nhất
Trường hợp xấu nhất xảy ra khi tiến trình phân vùng luôn chọn phần tử lớn nhất hoặc nhỏ nhất làm trục. Nếu xem xét chiến lược phân vùng trong đó phần tử cuối cùng luôn được chọn làm trục xoay, trường hợp xấu nhất sẽ xảy ra khi mảng đã được sắp xếp theo thứ tự tăng hoặc giảm. Sau đây là sự tái diễn cho trường hợp xấu nhất.
T(n) = T(0) + T(n-1) + (n)which is equivalent to T(n) = T(n-1) + (n)Giải pháp cho sự tái diễn trên là (n2).
Trường hợp tốt nhất
Trường hợp tốt nhất xảy ra khi quá trình phân vùng luôn chọn phần tử ở giữa làm trục. Sau đây là sự tái diễn cho trường hợp tốt nhất.
T(n) = 2T(n/2) + (n)Giải pháp cho sự lặp lại ở trên là (nLogn). Nó có thể được giải quyết bằng cách sử dụng trường hợp 2 của Định lý Master.
Trường hợp trung bình
Để phân tích trường hợp trung bình, ta cần xem xét tất cả các hoán vị có thể có của mảng và tính toán thời gian thực hiện cho mỗi hoán vị trông không dễ dàng.
Ta có thể hiểu về trường hợp trung bình bằng cách xem xét trường hợp khi phân hoạch đặt O (n / 9) phần tử trong một tập hợp và O (9n / 10) phần tử trong tập hợp khác. Sau đây là sự tái diễn cho trường hợp này.
T(n) = T(n/9) + T(9n/10) + (n)Giải pháp của sự tái diễn ở trên cũng là O (nLogn):
Mặc dù độ phức tạp về thời gian trong trường hợp xấu nhất của QuickSort là O (n2), cao hơn nhiều thuật toán sắp xếp khác như Merge Sort và Heap Sort, QuickSort trong thực tế nhanh hơn vì vòng lặp bên trong của nó có thể được triển khai hiệu quả trên hầu hết các kiến trúc và hầu hết các dữ liệu thế giới.
QuickSort có thể được thực hiện theo nhiều cách khác nhau bằng cách thay đổi sự lựa chọn của trục, để hạn chế tối đa trường hợp xấu nhất xảy ra đối với một loại dữ liệu nhất định. Tuy nhiên, sắp xếp hợp nhất thường được ưu tiên hơn trong trường hợp dữ liệu lớn và được lưu trữ trong bộ nhớ ngoài.
QuickSort có ổn định không?
Việc triển khai mặc định thường không ổn định. Tuy nhiên, bất kỳ thuật toán sắp xếp nào cũng có thể được ổn định nếu ta coi các chỉ mục là tham số so sánh.
QuickSort có In-place không?
Theo định nghĩa, QuickSort đủ điều kiện là một thuật toán sắp xếp In-place vì nó chỉ sử dụng thêm không gian để lưu trữ các lệnh gọi hàm đệ quy chứ không phải để thao tác đầu vào.
QuickSort 3 chiều là gì?
Trong thuật toán QuickSort đơn giản, chọn một phần tử làm pivot, phân vùng mảng xung quanh pivot và lặp lại cho các mảng con ở bên trái và bên phải của pivot.
Hãy xem xét một mảng có nhiều phần tử dư thừa. Ví dụ: {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}. Nếu 4 được chọn làm trục trong Simple QuickSort, ta chỉ sửa một 4 và xử lý đệ quy các lần xuất hiện còn lại. Trong 3 Way QuickSort, một mảng arr [l..r] được chia thành 3 phần:
arr [l..i]phần tử nhỏ hơn pivot.arr [i + 1..j-1]các phần tử bằng pivot.arr [j..r]phần tử lớn hơn pivot.
Tại sao QuickSort được ưu tiên hơn MergeSort trong sắp xếp Mảng?
QuickSort là thuật toán sắp xếp tại chỗ (tức là không yêu cầu thêm dung lượng) trong khi MergeSort yêu cầu thêm O (N) bộ nhớ, N biểu thị kích thước mảng có thể khá lớn. Việc phân bổ và loại bỏ không gian thừa được sử dụng để sắp xếp hợp nhất làm tăng thời gian chạy của thuật toán.
So sánh độ phức tạp trung bình, ta thấy rằng cả hai kiểu sắp xếp đều có độ phức tạp trung bình O (NlogN) nhưng các hằng số khác nhau. Đối với mảng, sắp xếp hợp nhất bị mất do sử dụng thêm không gian lưu trữ O (N).
Hầu hết các triển khai thực tế của QuickSort đều sử dụng phiên bản ngẫu nhiên. Phiên bản ngẫu nhiên có độ phức tạp thời gian dự kiến là O (nLogn). Trường hợp xấu nhất cũng có thể xảy ra trong phiên bản ngẫu nhiên, nhưng trường hợp xấu nhất không xảy ra đối với một mẫu cụ thể (như mảng được sắp xếp) và QuickSort ngẫu nhiên hoạt động tốt trong thực tế.
QuickSort cũng là một thuật toán sắp xếp thân thiện với bộ nhớ cache vì nó có vị trí tham chiếu tốt khi được sử dụng cho các mảng. QuickSort cũng là đệ quy đuôi, do đó tối ưu hóa cuộc gọi đuôi được thực hiện.
Tại sao MergeSort được ưu tiên hơn QuickSort cho các Danh sách được Liên kết?
Trong trường hợp danh sách liên kết, trường hợp này khác nhau chủ yếu do sự khác biệt trong phân bổ bộ nhớ của mảng và danh sách liên kết. Trong danh sách liên kết, chúng ta có thể chèn các mục vào giữa trong O (1) không gian phụ và O (1) thời gian. Do đó hoạt động hợp nhất của sắp xếp hợp nhất có thể được thực hiện mà không có thêm dung lượng cho danh sách được liên kết.
Trong mảng, chúng ta có thể thực hiện truy cập ngẫu nhiên vì các phần tử liên tục trong bộ nhớ. Giả sử chúng ta có một mảng A số nguyên (4 byte) và đặt địa chỉ của A [0] là x thì để truy cập A [i], chúng ta có thể truy cập trực tiếp vào bộ nhớ tại (x + i * 4).
Không giống như mảng, chúng ta không thể thực hiện truy cập ngẫu nhiên trong danh sách liên kết. QuickSort yêu cầu rất nhiều loại quyền truy cập. Trong danh sách liên kết để truy cập chỉ mục thứ i, chúng ta phải di chuyển từng nút từ đầu đến nút thứ i vì chúng ta không có khối bộ nhớ liên tục. Do đó, chi phí tăng lên để sắp xếp nhanh chóng. MergeSort truy cập dữ liệu một cách tuần tự và nhu cầu truy cập ngẫu nhiên là thấp.
QuickSort được đánh giá là có hiệu năng mạnh mẽ nhất trong tất cả các loại thuật toán sắp xếp phổ biến hiện nay như Bubble Sort, Insertion Sort, Selection Sort,… Nó cung cấp khả năng sắp xếp danh sách dữ liệu cực nhanh và chính xác. Bởi vậy mà khi nhắc đến các thuật toán quen thuộc trong lập trình, người ta nhớ ngay tới cái tên QuickSort.
Câu hỏi thường gặp
Tại sao Quick Soft được gọi là thuật toán sắp xếp nhanh?
Cái tên “Quick Soft” xuất phát từ thực tế là, sắp xếp nhanh có khả năng sắp xếp danh sách các phần tử dữ liệu nhanh hơn đáng kể (nhanh hơn hai lần hoặc ba lần) so với bất kỳ thuật toán sắp xếp thông thường nào .
Tại sao QuickSort không ổn định?
QuickSort là một thuật toán không ổn định
vì chúng ta hoán đổi các phần tử theo vị trí của trục (mà không xem xét vị trí ban đầu của chúng)
Lời kết
Trên đây, Vietnix đã cùng bạn tìm hiểu về cách triển khai Thuật toán sắp xếp nhanh Quick Sort cho các môi trường ngôn ngữ lập trình khác nhau từ C++14, Java, Python cho đến C#, Javascript. Mong rằng qua bài viết này, bạn sẽ hiểu hơn về Quick Sort và sớm “nắm” thuật toán này trong lòng bàn tay.
