Làm việc với dữ liệu set trong Python thường đòi hỏi các thao tác như hợp, giao, hiệu… Nắm vững các toán tử set là chìa khóa để xử lý hiệu quả các vấn đề này. Trong bài viết này, mình sẽ hướng dẫn chi tiết về các toán tử set trong Python phổ biến, giúp bạn thao tác dữ liệu set một cách dễ dàng và chuyên nghiệp.
Các điểm chính
Đọc xong bài viết, bạn sẽ:
- Thành thạo cách sử dụng các phép toán cơ bản trên set: Bạn sẽ biết cách dùng các toán tử như hợp (union), giao (intersection), trừ (difference), và symmetric difference để kết hợp và thao tác với các tập hợp một cách dễ dàng.
- Biết cách kiểm tra mối quan hệ subset giữa các set: Bạn sẽ học được cách xác định một set có phải là tập con của set khác hay không, một kỹ năng quan trọng khi làm việc với dữ liệu phức tạp.
- Có thể áp dụng kiến thức vào thực tế qua ví dụ cụ thể: Bạn sẽ được củng cố kiến thức thông qua các ví dụ minh họa rõ ràng, giúp bạn dễ dàng hình dung cách sử dụng các toán tử set trong các tình huống thực tế.
- Giới thiệu về dịch vụ VPS Vietnix – Giải pháp tốc độ vượt trội và xử lý mạnh mẽ.
Toán tử set trong Python
Các toán tử Set trong Python là các ký hiệu và hàm đặc biệt cho phép bạn thực hiện nhiều phép toán khác nhau trên các set, chẳng hạn như hợp, giao, hiệu và hiệu đối xứng. Các toán tử set trong Python cung cấp một cách để kết hợp, so sánh và sửa đổi các set.
Phép hợp của set trong Python
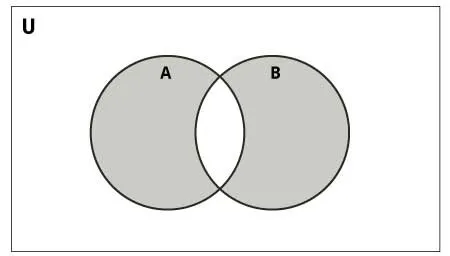
Phép hợp của hai set là một set mới chứa tất cả các phần tử riêng biệt có trong set A, hoặc trong set B, hoặc trong cả hai. Ví dụ:
{1, 2} ∪ {2, 3} = {1, 2, 3}
Hình ảnh sau đây minh họa phép hợp của hai set:
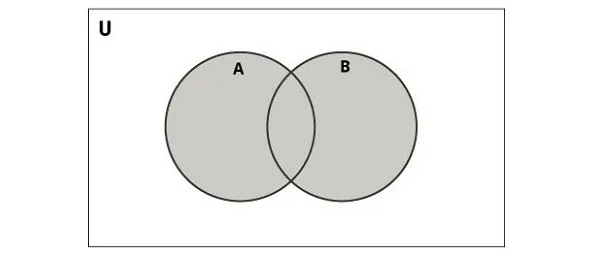
Trong Python, bạn có thể thực hiện phép hợp bằng cách sử dụng hàm union() hoặc toán tử |. Thao tác này kết hợp các phần tử của hai set, loại bỏ các phần tử trùng lặp, kết quả trả về là một set mới chứa tất cả các phần tử duy nhất từ cả hai set ban đầu.
Đoạn code sau đây sử dụng toán tử | và hàm union(), để trả về hợp của hai set:
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 45, 73}
#Sử dụng hàm union
union_set1 = set1.union(set2)
# Sử dụng toán tử set trong Python, cụ thể là toán tử "|"
union_set2 = set3 | set4
print('Hợp của set1 và set2 là', union_set1)
print('Hợp của set3 và set4 là', union_set2)Sau khi thực thi đoạn code trên, màn hình sẽ hiển thị:
Hợp của set1 và set2 là {1, 2, 3, 4, 5}
Hợp của set3 và set4 là {73, 6, 8, 9, 45}
Giải thích:
set1,set2,set3vàset4: được khởi tạo với các giá trị khác nhau.union_set1 = set1.union(set2): Dòng này sử dụng hàmunion()để tìm hợp củaset1vàset2. Kết quả được gán cho biếnunion_set1.union_set2 = set3 | set4: Dòng này sử dụng toán tử|(một trong các toán tử set trong Python) để thực hiện phép hợp giữaset3vàset4. Kết quả được lưu vào biếnunion_set2.- Các lệnh
print(): in kết quả ra màn hình
Toán tử giao của set trong Python
Phép giao (intersection) của hai set A và B, ký hiệu là A∩B, bao gồm tất cả các phần tử chung của cả A và B. Ví dụ:
{1, 2}∩{2, 3} = {2}
Biểu đồ dưới đây minh họa phép giao của hai set:
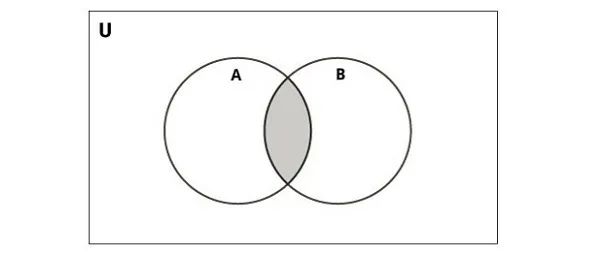
Python cung cấp hàm intersection() hoặc toán tử set trong Python & để thực hiện phép toán này. Kết quả của phép giao là một set mới, set kết quả này chỉ chứa các phần tử xuất hiện trong cả hai set ban đầu.
Ví dụ sau sử dụng toán tử & và hàm intersection(), và trả về giao của hai set:
tap_hop_so_nguyen_duong_nho = {1, 2, 3, 4, 5}
tap_hop_so_chan = {2, 4, 6, 8, 10}
tap_hop_so_le = {1,3,5,7,9}
tap_hop_so_nguyen_to = {2,3,5,7,11}
# Sử dụng hàm intersection()
giao_1 = tap_hop_so_nguyen_duong_nho.intersection(tap_hop_so_chan)
# Sử dụng toán tử &
giao_2 = tap_hop_so_le & tap_hop_so_nguyen_to
print('Phần giao của tập số nguyên dương nhỏ và tập số chẵn:', giao_1)
print('Phần giao của tập số lẻ và tập số nguyên tố:', giao_2)Khi chạy chương trình, các bạn sẽ nhận được kết quả là các set chứa những phần tử thuộc về cả hai tập hợp tương ứng. Kết quả:
Phần giao của tập số nguyên dương nhỏ và tập số chẵn: {2, 4}
Phần giao của tập số lẻ và tập số nguyên tố: {3, 5, 7}
Giải thích:
- Đầu tiên, các set (
tap_hop_so_nguyen_duong_nho,tap_hop_so_chan,tap_hop_so_le,tap_hop_so_nguyen_to) được khai báo, mô phỏng các tập hợp số khác nhau. giao_1: được tính bằng cách gọi phương thứcintersection()củatap_hop_so_nguyen_duong_nho, truyềntap_hop_so_chanlàm đối số.giao_2: được tính bằng cách sử dụng toán tử&giữatap_hop_so_levàtap_hop_so_nguyen_to. Toán tử&là cách viết tắt để tìm phần giao của hai set.
Phép trừ của set trong Python
Phép trừ (difference) giữa hai set trả về một set mới chứa các phần tử có trong set thứ nhất nhưng không có trong set thứ hai. Định nghĩa này được mô tả như sau: set A − B bao gồm các phần tử có trong A nhưng không có trong B. Ví dụ:
Nếu A = {1, 2, 3} và B = {3, 5}, thì A − B = {1, 2}.
Hình ảnh sau minh họa phép trừ của hai set:
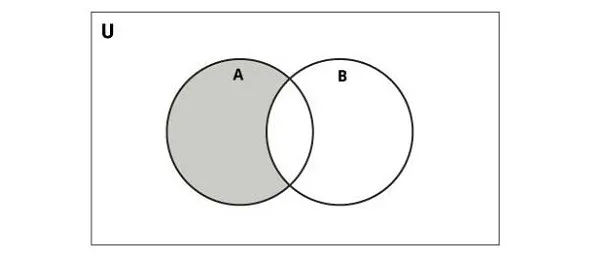
Trong Python, bạn có thể sử dụng hàm difference() hoặc toán tử – để thực hiện phép toán này. Set kết quả sẽ chứa các phần tử chỉ có trong set đầu tiên. Thay vì sử dụng các số đơn giản, hãy xem xét ví dụ thực tế hơn, chẳng hạn như so sánh các loại trái cây có trong hai giỏ hàng khác nhau.
gio_trai_cay_A = {"táo", "cam", "chuối"}
gio_trai_cay_B = {"chuối", "lê", "dứa"}
gio_trai_cay_C = {'xoài', 'ổi', 'mận'}
gio_trai_cay_D = {'mận', 'ổi', 'dâu tây'}
# Sử dụng hàm difference()
trai_cay_chi_co_trong_A = gio_trai_cay_A.difference(gio_trai_cay_B)
# Sử dụng toán tử -
trai_cay_chi_co_trong_C = gio_trai_cay_C - gio_trai_cay_D
print('Các loại trái cây chỉ có trong giỏ A:', trai_cay_chi_co_trong_A)
print('Các loại trái cây chỉ có trong giỏ C:', trai_cay_chi_co_trong_C)Khi chạy đoạn code trên, ta có kết quả:
Các loại trái cây chỉ có trong giỏ A: {‘táo’, ‘cam’}
Các loại trái cây chỉ có trong giỏ C: {‘xoài’}
Giải thích:
- Hai set
gio_trai_cay_Avàgio_trai_cay_Bđược khởi tạo, chứa tên các loại trái cây. trai_cay_chi_co_trong_A = gio_trai_cay_A.difference(gio_trai_cay_B): Hàmdifference()được gọi trêngio_trai_cay_A, vớigio_trai_cay_Blà tham số. Kết quả trả về là một set mới chứa các loại trái cây chỉ có ởgio_trai_cay_Amà không có ởgio_trai_cay_B.trai_cay_chi_co_trong_C = gio_trai_cay_C - gio_trai_cay_D: Ở đây ta thực hiện phép trừ trực tiếp 2 set sử dụng toán tử set-- Hai dòng
printcuối cùng in kết quả ra màn hình. - Hai set
gio_trai_cay_Cvàgio_trai_cay_Dđược khởi tạo để làm ví dụ khác, các giá trị set là khác nhau. trai_cay_chi_co_trong_A = gio_trai_cay_A.difference(gio_trai_cay_B): tính toán và gán các phần tử khác nhau.
Symmetric difference của set trong Python
Phép tìm sự khác biệt đối xứng của hai set bao gồm các phần tử chỉ xuất hiện trong một trong hai set, nhưng không xuất hiện trong cả hai. Phép khác biệt đối xứng của hai set A và B được ký hiệu là “A Δ B” và được định nghĩa như sau:
A Δ B = (A − B) ⋃ (B − A)
Nghĩa là, kết quả sẽ bao gồm các phần tử chỉ có trong A mà không có trong B, hợp (⋃) với các phần tử chỉ có trong B mà không có trong A.
Ví dụ: Nếu A = {1, 2, 3, 4, 5, 6, 7, 8} và B = {1, 3, 5, 6, 7, 8, 9}, thì A Δ B = {2, 4, 9}. Biểu đồ sau đây minh họa phép tìm sự khác biệt đối xứng giữa hai set:
Ví dụ
Trong Python, bạn có thể sử dụng hàm symmetric_difference() hoặc toán tử ^ để thực hiện phép toán này. Kết quả trả về là một set mới chứa các phần tử chỉ thuộc về một trong hai set ban đầu.
Để dễ hình dung hơn, chúng ta xem xét một ví dụ khác với set:
trai_cay_mua_he = {"xoài", "dưa hấu", "mận", "vải"}
trai_cay_mua_dong = {"cam", "quýt", "mận", "bưởi"}
# Sử dụng hàm symmetric_difference()
khac_biet_1 = trai_cay_mua_he.symmetric_difference(trai_cay_mua_dong)
# Sử dụng toán tử ^
khac_biet_2 = trai_cay_mua_he ^ trai_cay_mua_dong
print('Các loại trái cây chỉ có trong một mùa (cách 1):', khac_biet_1)
print('Các loại trái cây chỉ có trong một mùa (cách 2):', khac_biet_2)Khi bạn chạy, màn hình sẽ hiển thị (kết quả có thể thay đổi thứ tự các phần tử, vì set không quan tâm thứ tự):
Các loại trái cây chỉ có trong một mùa (cách 1): {‘xoài’, ‘dưa hấu’, ‘vải’, ‘cam’, ‘quýt’, ‘bưởi’}
Các loại trái cây chỉ có trong một mùa (cách 2): {‘xoài’, ‘dưa hấu’, ‘vải’, ‘cam’, ‘quýt’, ‘bưởi’}
Giải thích:
- Hai
settrai_cay_mua_hevàtrai_cay_mua_dongđược khởi tạo, chứa tên các loại trái cây. khac_biet_1được tính bằng cách gọi hàmsymmetric_difference()trênsettrai_cay_mua_he, truyềnsettrai_cay_mua_dongvào.khac_biet_2được tính tương tự nhưng sử dụng toán tử^.- Cả hai kết quả giống nhau và trả về tập hợp những loại trái cây chỉ có trong một trong hai
set.
Kiểm tra subset trong Python
Trong Python, bạn có thể kiểm tra xem một set có phải là tập con của một set khác hay không bằng cách sử dụng hàm issubset() hoặc toán tử <=. Một set A được coi là tập con của set B nếu tất cả các phần tử của A đều có mặt trong B.
Hãy xem xét một ví dụ gần gũi hơn:
nhom_mau_AB = {"A", "B", "AB", "O"} # Tập hợp các nhóm máu
nhom_mau_nguoi_1 = {"A", "O"}
nhom_mau_nguoi_2 = {"C", "D"} # các nhóm máu không tồn tại trong thực tế
# Kiểm tra với issubset()
kiem_tra_1 = nhom_mau_nguoi_1.issubset(nhom_mau_AB)
# Kiểm tra với <=
kiem_tra_2 = nhom_mau_nguoi_2 <= nhom_mau_AB
print('Nhóm máu của người 1 có phải là tập con của tập các nhóm máu?', kiem_tra_1)
print('Nhóm máu của người 2 có phải là tập con của tập các nhóm máu?', kiem_tra_2)Kết quả in ra sẽ cho biết:
nhom_mau_nguoi_1 LÀ tập con của nhom_mau_AB vì tất cả nhóm máu trong nhom_mau_nguoi_1 tồn tại trong nhom_mau_AB
nhom_mau_nguoi_2 KHÔNG phải là tập con nhom_mau_AB vì có phần tử không nằm trong nhom_mau_AB.
Giải thích code:
nhom_mau_ABlà một set chứa tất cả các nhóm máu.nhom_mau_nguoi_1vànhom_mau_nguoi_2là các set biểu diễn nhóm máu của hai người khác nhau (Lưu ý ví dụ 2 các nhóm máu đó không tồn tại).kiem_tra_1: kiểm tra xemnhom_mau_nguoi_1có phải là tập con củanhom_mau_ABkhông, bằng cách sử dụng hàmissubset().kiem_tra_2: thực hiện kiểm tra tương tự, nhưng sử dụng toán tử<=.
Dịch vụ VPS Vietnix - Giải pháp tốc độ vượt trội và xử lý mạnh mẽ
Khi mua VPS từ Vietnix, bạn sẽ sở hữu một dịch vụ với hiệu suất vượt trội, tối ưu hóa tốc độ tải trang và mang lại trải nghiệm người dùng mượt mà. Với công nghệ ảo hóa hiện đại và giao diện quản trị dễ sử dụng, bạn có thể tùy chỉnh và quản lý máy chủ theo nhu cầu và quy mô dự án. Dịch vụ còn hỗ trợ sao lưu dữ liệu tự động miễn phí mỗi tuần, bảo vệ dữ liệu và đảm bảo khả năng phục hồi nhanh chóng. Hệ thống VPS của Vietnix hỗ trợ đa dạng các hệ điều hành, từ Windows Server đến các bản phân phối Linux như Ubuntu, CentOS, giúp bạn tự do lựa chọn nền tảng phù hợp.
Dịch vụ VPS AMD của Vietnix mang đến hiệu suất xử lý vượt trội, giúp website của bạn hoạt động ổn định và tăng trưởng mạnh mẽ. Dịch vụ sử dụng ổ cứng NVMe Enterprise, dịch vụ này cho phép truy cập và xử lý dữ liệu với tốc độ cực kỳ nhanh chóng, đáp ứng mọi yêu cầu cao về hiệu suất. Với khả năng quản lý và tùy chỉnh máy chủ linh hoạt, dịch vụ này phù hợp với mọi loại hình doanh nghiệp cần hiệu suất cao và sự ổn định lâu dài.
Thông tin liên hệ:
- Hotline: 18001093
- Email: sales@vietnix.com.vn
- Địa chỉ: 265 Hồng Lạc, Phường Bảy Hiền, Thành phố Hồ Chí Minh.
- Website: https://vietnix.vn/
Vậy là chúng ta đã cùng nhau khám phá các toán tử set mạnh mẽ trong Python rồi! Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách sử dụng các toán tử như hợp, giao, trừ và symmetric difference để xử lý dữ liệu một cách hiệu quả. Nắm vững những kiến thức này sẽ là một lợi thế lớn khi bạn làm việc với các bài toán liên quan đến tập hợp dữ liệu trong Python đó.
Mọi người cũng đọc











